Law of Exponents Multiple Choice Questions: Question: (32)2 x (32)4 / (27)4 ? (a) 1 (b) 2 (c) 3 (d)...
Category - Mathematics
Surface Area and Volume Quiz with answers
Surface Area & Volume Ratio multiple choice questions: The dimensions of a metallic cuboid are...
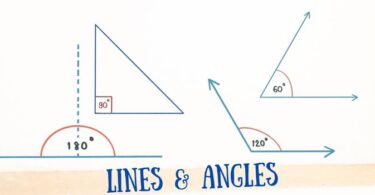
Lines and Angles Questions and Answers
Quiz of Lines and Angles: Question: If two straight lines have no points in common, they are (a)...
Discrete Mathematics Quiz
Discrete mathematics questions and answers: Question: Which of the following is a Proposition? (a)...
Euclidean Geometry Quiz with Answers
Euclid Geometry Questions and Answers: Ques. The three steps from solids to points are : (a) Solids...
Mean, Median, Mode quiz
Math questions on Mean, Mode and Median: Ques. Which of the following average is most affected of...
General Maths Quiz
Basic and general Mathematics quiz questions with answers What fraction of a millimeter is a...
Area of Parallelograms and Triangles Worksheet
MCQ on Areas of parallelograms and Triangles Ques. A parallelogram ABCD and a rectangle ABPQ are on...
Quadratic Equations Exercise
Quadratic Equations Test: Ques: The roots of the equation ix2 – 4x – 4i = 0 are (a) –2i (b) 2i (c)...
Square Root Questions
Square and Square Root Practice Test: The largest of four digit numbers which is a perfect square...
multiple choice questions on Matrices and Determinants
MCQ on Matrices and Determinants: If the system of equations, x + 2y – 3z = 1, (k + 3)z = 3, (2k +...
Binomial Theorem practice questions
Binomial Theorem Quiz: Ques. The total number of terms in the expansion of (x + a)100 + (x – a)100...
Quadrilateral test questions
MCQ on understanding Quadrilaterals: Question: The diagonals do not necessarily bisect the interior...
Cube Root Problems
Cubes and Cube Root practice worksheet: Ques. Which of the following are cubes of even natural...
Set Theory Questions and Answers
Set Theory Problems with answers: If two sets A and B have 99 elements in common, then the number...
Mathematical Induction questions with answers
Mathematical induction and Divisibility problems: Ques. For all positive integral values of n, 32n...
Polynomials Questions and Answers
Problem questions on polynomials (Algebra): Question: If (2x – 1) is a factor of both 6x2 + ax – 4...
Coordinate Geometry Questions and Answers
Important Questions for Coordinate Geometry (Mathematics): Ques. If x is a positive integer such...